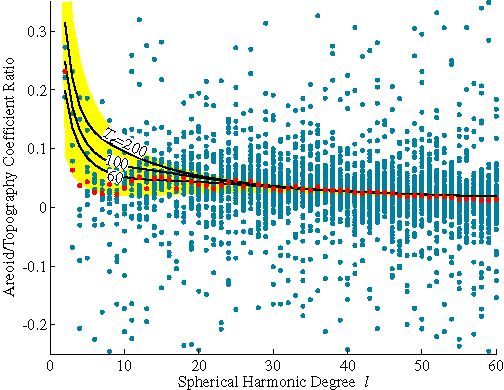
Interestingly, we can devise a mass distribution model that exactly matches the observed topography and geoid of a planet regardless of what properties of planetary density and lithospheric strength we may choose (see, e.g., the section on Planetary Loading Processes). Since density and strength properties are often estimated from relationships of gravity to topography, this poses a conundrum: We cannot determine uniquely what these properties truly are unless we impose some additional constraint on the solution. Two differing approaches are commonly taken to resolve the problem. One approach is to model the admittance, which is an averaged ratio of the gravity (or geoid) divided by topography in the spectral domain. Averages of the geoid-topography ratio of Mars (red circles) cancel the effects of uncorrelated loads in the individual spherical harmonic coefficients (blue circles), resulting in a curve that closely approximates the model prediction for pure surface loading (yellow region, encompassing models of surface load response for lithospheric thickness T_e=50 to 200 km, crustal thickness T_c=10 to 160 km, crustal density r₀=2400 to 3200 kg m^-3, and mantle density r₁=3300 to 3800 kg m^-3).

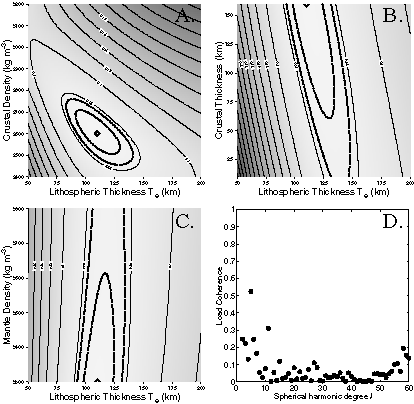
A better alternative is to assume that surface and internal loads are uncorrelated, and find the model parameters that minimize the coherence (i.e., squared correlation coefficient) of the predicted loads [Lowry and Zhong, 2003]. Obviously, loads are not always truly uncorrelated, but the processes by which they correlate depend on location and scale such that the global aggregate behavior simulates that of two uncorrelated fields. An incorrect isostatic model parameterization cannot reduce the apparent correlation at the particular locations and scales where the two fields are truly correlated without introducing a larger (spurious) apparent correlation of the fields at all other locations and scales. Consequently, the coherence of predicted load fields is quite sensitive to model parameters such as density and T_e. The figure at left depicts the global coherence of predicted Martian load fields as a function of T_e, crustal density, crustal thickness and mantle density. The minimum coherence model is indicated by diamonds, and one-sigma and two-sigma confidence intervals are shown as thick dashed lines. The coherence of loads is very insensitive to assumed crustal thickness and mantle density, so we cannot constrain those by this method. However, lithospheric thickness and crustal density are tightly constrained, with best estimates of around T_e=110 km and r₀=2600 kg m^-3. The wavelength dependence for the minimum coherence model (part D of the figure) still shows evidence of enhanced correlation of surface and internal loads at the wavelengths where processes might be expected to produce such correlation. This enhanced correlation at particular wavelengths may be used in turn to assess spatial variations in planetary properties by treating them as deviations from the global average.